【C#】ベジェ曲線を計算する

ベジェ曲線 - Wikipedia

wiki より計算式を拝借して、ベジェ曲線を計算するクラスを作成しました

使い方

Transform の座標を使ってやる場合はこんなふうに

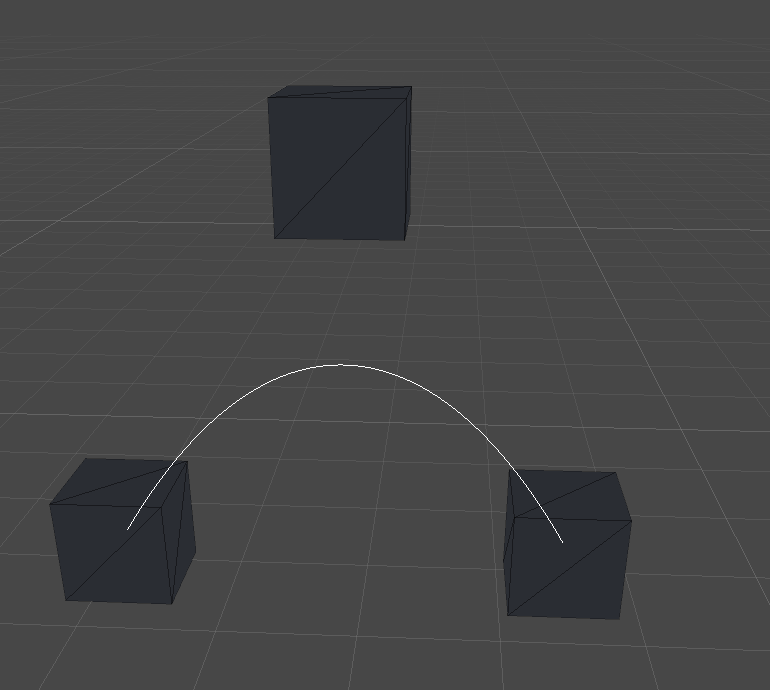
public class SampleMonoBehaviour : MonoBehaviour
{
    [SerializeField]
    private Transform[] _transforms;

    private void OnDrawGizmos()
    {
        if (_transforms == null || _transforms.Length <= 1)
            return;

        var a = _transforms.Select(t => t.position).ToArray();
        var prev = _transforms[0].position;
        for (var i = 0f; i <= 1f; i += 0.01f)
        {
            var pos = BezierCurve.Eval(a, i);
            Gizmos.DrawLine(prev, pos);
            prev = pos;
        }
    }
}

予め座標が固定されているなら
インスタンスを作成して Eval を呼び出します

var curve = new BezierCurve(new []
{
    new Vector3(0, 0, 0),
    new Vector3(0, 1f, 0),
    new Vector3(1f, 0, 0),
});

var pos = curve.Eval(0.5f);

コード

using System;
using UnityEngine;

[Serializable]
public class BezierCurve
{
    private Vector3[] _positions;

    public BezierCurve(Vector3[] positions)
    {
        _positions = positions;
    }

    public Vector3 Eval(float t)
    {
        return Eval(_positions, t);
    }

    public static Vector3 Eval(Vector3[] pos, float t)
    {
        if (pos == null || pos.Length < 1)
            return Vector3.zero;

        var length = pos.Length;
        if (length == 1)
            return pos[0];

        var r = Vector3.zero;
        for (var i = 0; i < length; i++)
            r += pos[i] * Bernstein(t, length - 1, i);

        return r;
    }

    /// <summary>
    /// バースタイン基底関数
    /// </summary>
    /// <returns></returns>
    private static float Bernstein(float t, int n, int i)
    {
        return nCr(n, i) * Mathf.Pow(t, i) * Mathf.Pow(1 - t, n - i);
    }

    /// <summary>
    /// n 個から r 個を取り出すときの組み合わせの数
    /// </summary>
    private static long nCr(int n, int r)
    {
        return Factorial(n) / (Factorial(r) * Factorial(n - r));
    }

    private static int Factorial(int i)
    {
        if (i <= 1)
            return 1;

        return i * Factorial(i - 1);
    }
}